[알고리즘] 하노이 탑 이동순서(백준 11729/파이썬)

필요한 개념:재귀함수

 

재귀함수란?

재귀호출이라고도 불리며 함수 안에서 자신을 다시 호출하여 작업을 수행하는 방식의 함수입니다. 
반복문을 사용하는 코드는 재귀 함수를 통해 구현하는 것이 가능합니다.

재귀 함수를 작성할때는 함수 내에서 다시 자신을 호출 한 후 그 함수가 끝날 때까지 함수 이후의

명령문이 수행되지 않기 때문에 무한루프를 방지하기 위하여 원하는 값을 얻으면 종료하거나 들어가는 인자값이

계속 변하는등 '종료조건'을 꼭 포함하여야 합니다.
재귀 함수는 메모리를 많이 차지 하기 때문에 재귀 함수를 많이 사용하면 스택 메모리가 커지고
호출하는 횟수가 많아지므로 스택오버플로우가 발생할 수 있습니다.

 

[문제]

 

 

[문제해결방법]

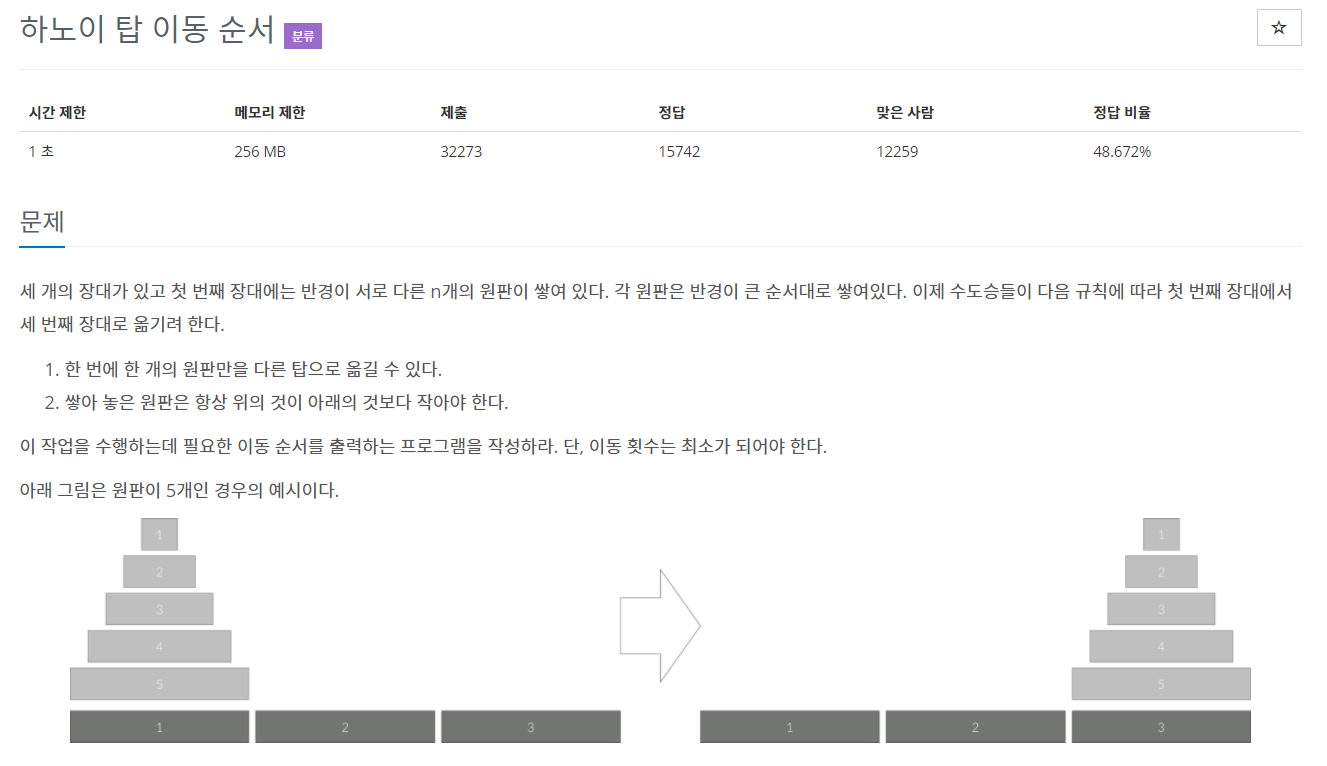
하노이의 탑은 시작 기둥에서 도착 기둥으로 모든 원판을 옮기는 것이 목표입니다.

조건은 작은 원판 위에 큰 원판이 올라갈 수 없다고 합니다.

기둥이 출발기둥: A, 보조기둥: B, 도착기둥: C 3개가 있고 원판이 6개 있을때 

마지막 원판이 도착지인 c에 가려면 각 원판을 처음 움직일 때는 아래의 그림처럼 각 원판의 도착지가 정해집니다.

 

 

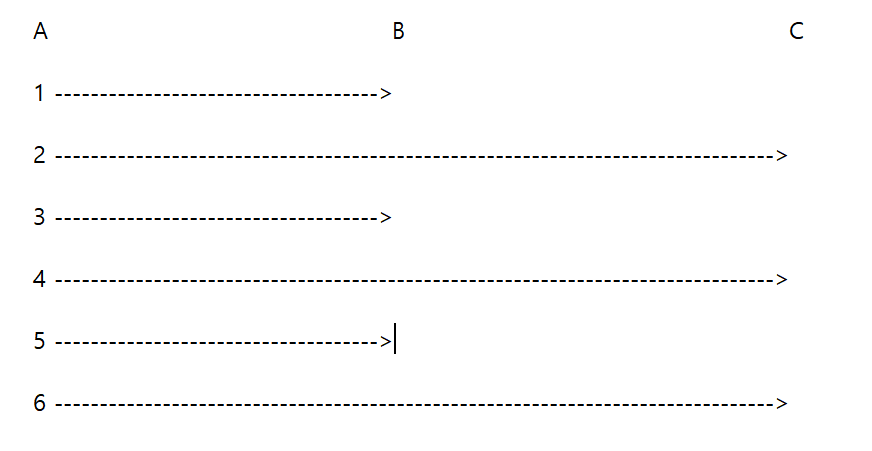
위에 그림처럼 원판을 이동할 때 처음에는

1원판: A -> B로 이동, 2원판: A ->C로 이동하고 3원판이 B기둥으로 이동하려는데

조건에 작은 원판 위에 큰 원반이 올라 갈 수 없으니 다시 1원판: B -> c로 이동하고 3원판: A -> B로 이동하게 됩니다.

 출발         도착

1원반 :   A     ->     B         

2원반 :   A     ->     C         

1원반 :   B      ->    C         

3원반 :   A     ->     B         

이런식으로 출발지와 도착지가 변경되는 코드를 짜면 됩니다.

출발지와 도착지가 계속 반복 되니까 이 부분을 재귀함수를 사용하면 됩니다.

 

[코드리뷰]

import sys

move =[]
#원판이 움직였을때 위치 값을 담아주기 위해서 리스트를 만듭니다.

          # 시작  도착
def hanoi(n, A, B, C):
       #     1  2  3
       # n=2 1  3  2
       # n=1 1  1  3
    if n==1:
        move.append([A,C])
        #원판이 한개 남았을때 움직인 값을 move에 저장합니다.
    else:
        hanoi(n-1,A,C,B)
        #n-1 = 2  1 3 2 
        #n-1 = 1  1 2 3 
        move.append([A,C])
        #움직인 값을 move에 저장합니다.
        hanoi(n-1,B,A,C)
        #그 다음 원판을 계산하기 위해 다시 하노이 함수를 호출합니다.

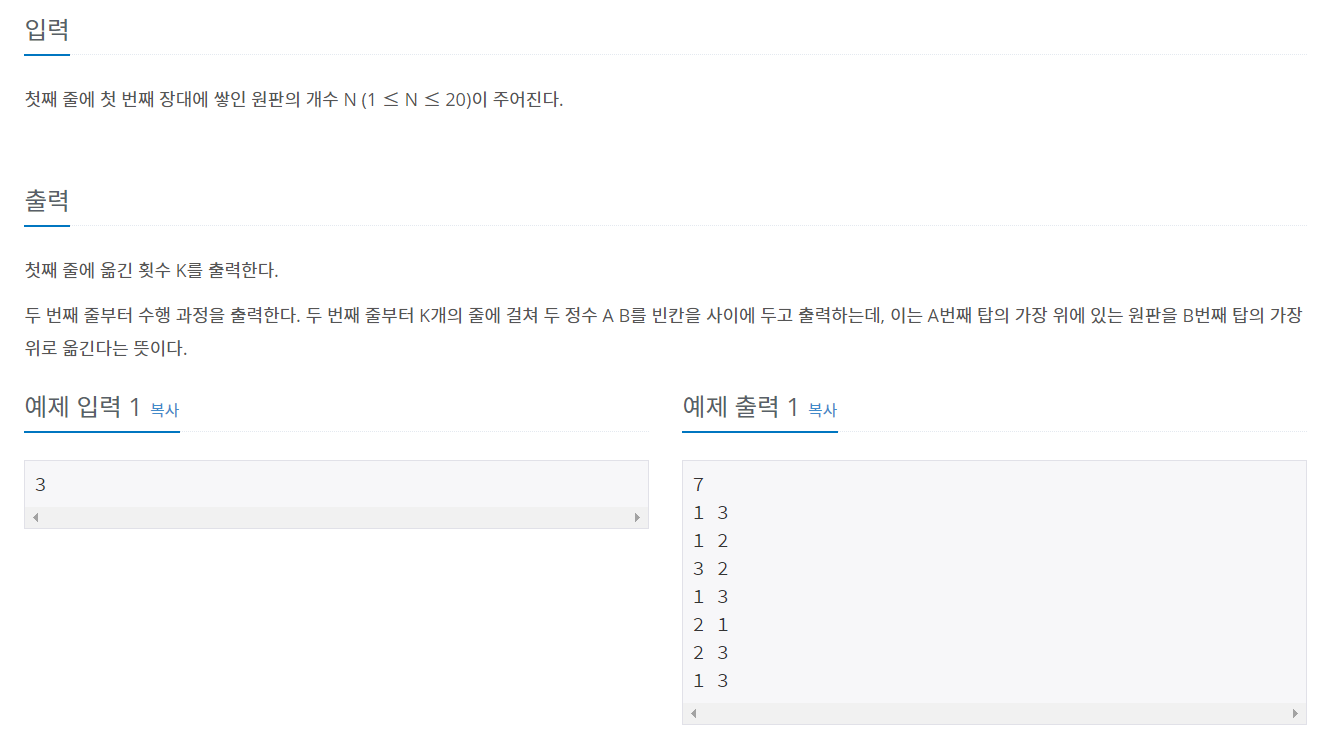
a=int(sys.stdin.readline())
#원판의 개수를 받는다
hanoi(a,1,2,3)
#하노이 함수를 호출한다
print(len(move))
#옮긴 횟수를 프린트하기 위해 move의 길이를 출력하여 줍니다.
print('\n'.join([' '.join(str(i) for i in row )for row in move]))
#move안에 있는 수(i, row)들을 문자열로 바꾸고 띄어쓰기를 넣고 줄을 바꿔 프린트 합니다.

 

[결과]

아래에 나오는 결과처럼 재귀 함수 호출을 많이 할수록 메모리 값이 커집니다.